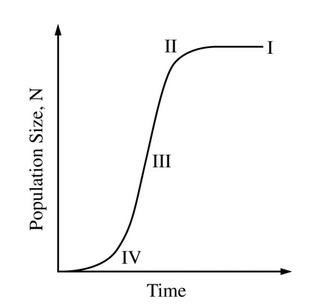
One model of a sustainable fisheries practice is for individual fish to be removed from a natural population at a rate equal to the highest possible growth rate of an ideal population. The graph above represents a population of bluefin tuna living along the Atlantic coast. At which labeled point in the graph is the population growth rate the highest?

In the graph, the population's growth rate reflects logistic growth. The growth rate initially increases but levels off as the population nears its carrying capacity. The carrying capacity is indicated by the horizontal line between II and I. The highest growth rate occurs at III. One way to mathematically interpret growth rate is to estimate the slope, \(\dfrac{\text{Population}}{\text{Time}}\). The slope at III is the steepest.