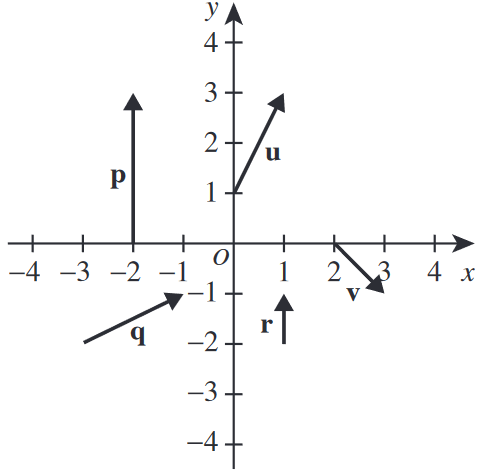
Representatives of vectors $\textbf{u}$, $\textbf{v}$, $\textbf{p}$, $\textbf{q}$, and $\textbf{r}$ are shown in the standard $(x,y)$ coordinate plane below.

One of the following vectors is equal to the vector $\textbf{u}+\textbf{v}$. Which one?

Summary Submit Skip Question

First, lets find the components of $\textbf{u}$ and $\textbf{v}$.

$$\textbf{u} = \lang 1,2 \rang$$ $$\textbf{v} = \lang 1,-1 \rang$$

Adding the components:

$$\textbf{u}+\textbf{v} = \lang 1+1, 2+(-1) \rang$$ $$\textbf{u}+\textbf{v} = \lang 2, 1 \rang$$

This corresponds to $\boxed{\textbf{q}}$.