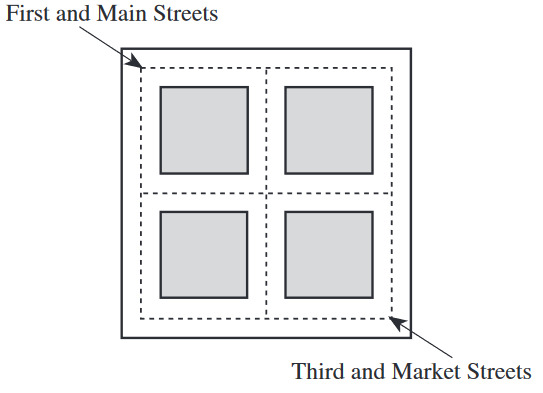
Using the street map shown below, you are directed to take a 4-block-long route to walk from First and Main Streets to Third and Market Streets. If each of the different 4-block-long routes consists of a unique sequence of streets, how many such routes could you take?

Summary Submit Skip Question

List out all of the options:

Right, Right, Down, Down

Right, Down, Right, Down

Right, Down, Down, Right

Down, Right, Down, Right

Down, Down, Right, Right

Down, Right, Right, Down

This is a permutation problem, where ordering does matter. We can think of having 4 total moves, where we wish to choose the different options of placing the two 'right' movements.

$${}_nP_r = \frac{n!}{(n-r)!}$$ $${}_4P_2 = \frac{4!}{(4-2)!}$$ $$= \frac{4!}{2!}$$ $$= \frac{4\cdot 3\cdot 2}{2}= 12$$

We need to remove redundancies, such as when we pick:

$$R_1, R_2, D_1, D_2 \text{ is equal to } R_2, R_1, D_2, D_1$$

We can divide the number we got from the permutation by 2, since there are two copies of every movement:

$$\frac{12}{2} = \boxed{6}$$

Grid movements can be solved with combinations.

$${}_nC_r = \frac{n!}{(n-r)!r!}$$ $${}_4C_2 = \frac{4!}{(4-2)!r!}$$ $$= \frac{4\cdot 3\cdot 2}{2\cdot 2}$$ $$= \boxed{6}$$