In the ellipse shown below, $\overline{AC}$ is the major axis with length 16 feet, $\overline{BD}$ is the minor axis with length 12 feet, and $E$ is the center. Point $F$ lies on side $\overline{BC}$ of the inscribed rhombus $ABCD$.

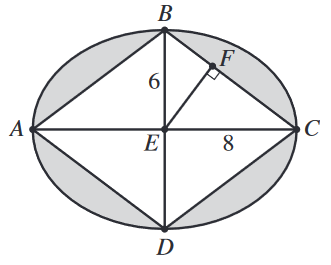
The eccentricity, $e$, of an ellipse is a measure of the flatness of the ellipse. The eccentricity of a circle is 0. The value of $e$ is given by the ratio $\dfrac{\sqrt{a^2-b^2}}{a}$, where $a$ and $b$ are half the lengths of the major and minor axes, respectively. Which of the following intervals contains the value of $e$ for this ellipse?

Summary Submit Skip Question

Although there is quite a lot of reading, we can just plug values into the given formula:

$$\frac{\sqrt{a^2-b^2}}{a}$$ $$\frac{\sqrt{(8)^2-(6)^2}}{8}$$ $$= \frac{\sqrt{64-36}}{8}$$ $$= \frac{\sqrt{28}}{8}$$ $$\approx 0.66$$