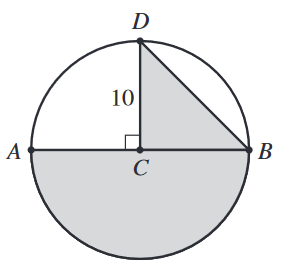
In the circle shown below, $C$ is the center, $\overline{AB}$ is a diameter, and $\overline{CD}$ is a radius of length 10 inches that is perpendicular to $\overline{AB}$. Which of the following values is closest to the area, in square inches, of the shaded region (the combined area of the semicircle and $\triangle{BCD}$) ?

Summary Submit Skip Question

The area of the semicircle is half of the area of the circle.

$$A_{\text{semicircle}} = \frac{1}{2}\pi r^2$$ $$A_{\text{semicircle}} = \frac{1}{2}\pi (10)^2 \approx 157 \text{ in}^2$$

The area of the triangle (note that the base and height are both radii of the circle):

$$A_{\text{triangle}} = \frac{1}{2}bh$$ $$A_{\text{triangle}} = \frac{1}{2}(10)(10) = 50 \text{ in}^2$$

The total area is the sum:

$$157 + 50 = \boxed{207}$$