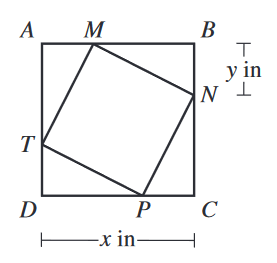
In the figure shown below, square $MNPT$ is inscribed in square $ABCD$. The length of $\overline{DC}$ is $x$ inches, and the length of $\overline{BN}$ is $y$ inches. In terms of $x$ and $y$, which of the following expressions gives the area, in square inches, of $MNPT$ ?

Summary Submit Skip Question

The sides of the smaller square are the hypotenuse of the triangles. The triangles have sides $x-y$ and $y$. Using the pythaogrean theorem:

$$a^2+b^2=c^2$$ $$(x-y)^2+y^2 = c ^2$$ $$=x^2-2xy+y^2+y^2 = c^2$$ $$c^2=\boxed{x^2-2xy+2y^2}$$

Since the area of a square is the side squared, $c^2$ equals the area of the smaller square.