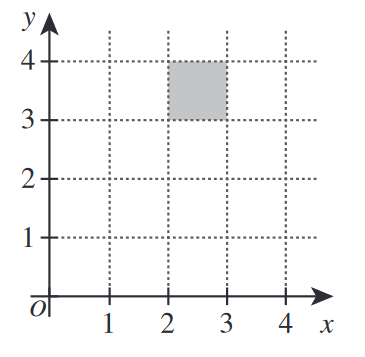
In the standard $(x,y)$ coordinate plane below, a shaded square is shown with vertices at $(2,3)$, $(2,4)$, $(3,3)$, and $(3,4)$. Two lines, $y=rx$ and $y=sx$, each intersect the shaded square at exactly 1 point. Given that $r\neq s$, what is the positive difference of $r$ and $s$ ?

Summary Submit Skip Question

A line starting at the origin can intersect at 1 point only if it goes through $(2,4)$ or $(3,3)$.

The corresponding slopes of these two lines would be $\dfrac{4}{2}$ and $\dfrac{3}{3}$.

$$\frac{4}{2} - \frac{3}{3}$$ $$2- 1 = \boxed{1}$$