In the standard \((x,y)\) coordinate plane below, \(\triangle{ABC}\) is bounded by \(\overline{AB}\), \(\overline{AC}\), and the \(y\)-axis. Which of the following values is closest to the area, in square coordinate units, of \(\triangle{ABC}\) ?
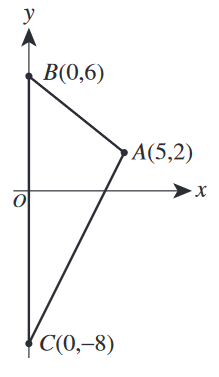
In the standard \((x,y)\) coordinate plane below, \(\triangle{ABC}\) is bounded by \(\overline{AB}\), \(\overline{AC}\), and the \(y\)-axis. Which of the following values is closest to the area, in square coordinate units, of \(\triangle{ABC}\) ?
